In the previous session we looked at identifying and measuring patterns of spatial autocorrelation (clustering) in data. If those patterns exist then there is potential to use them to our advantage by ‘pooling’ the data for geographical sub-spaces of the map, creating local summary statistics for those various parts of the map, and then comparing those statistics to look for spatial variation (spatial heterogeneity) across the map and in the data. The method we shall use here is found in GWmodel – an R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models. These are geographically weighted statistics.
Broadly, there are three parts to this session, which are:
The last of these is not directly related to Geographically Weighted Statistics and can be skipped if time is short or if the previous parts were enough for you ‘to chew on’.
The idea behind geographically weighted statistics is simple. For example, instead of calculating the (global) mean average for all of the data and the whole map, a series of (local) averages are calculated for various sub-spaces within the map. Those location specific averages can then be compared.
It works likes this. Imagine a point location, \(i\), at position \((u_i, v_i)\) on the map. To calculate the local statistic:
Let’s see this in action, beginning by ensuring the necessary packages are installed and required. As with previous sessions, you might start by opening the R Project that you created for these classes.
installed <- installed.packages()[,1]
pkgs <- c("colorspace", "cols4all", "GWmodel", "proxy", "sf", "sp",
"tidyverse", "tmap")
install <- pkgs[!(pkgs %in% installed)]
if(length(install)) install.packages(install, dependencies = TRUE)
invisible(lapply(pkgs, require, character.only = TRUE))
sp and its associated packages have been retired in favour of sf and others. The reason for requiring it here is that the GWmodel package that we will use for the geographically weighted statistics still uses it.
We will use the same data as in the previous session but confine the analysis to the Western Cape of South Africa. This is largely to reduce run times but there is another reason that I shall return to presently.
download.file("https://github.com/profrichharris/profrichharris.github.io/blob/main/MandM/workspaces/wards.RData?raw=true", "wards.RData", mode = "wb", quiet = TRUE)
load("wards.RData")
wards |>
filter(ProvinceNa == "Western Cape") ->
wcape_wardsThe calculation points for the geographically weighted statistics will be the ward centroids. A slight complication here is that GWmodel presently is built around the elder sp not sf formats for handling spatial data in R so the wards need to be converted from the one format to the other.
wcape_wards_sp <- as_Spatial(wcape_wards)We can see that wcape_wards is of class sf,
class(wcape_wards)[1] "sf" "data.frame"whereas wcape_wards_sp is now of class SpatialPolygonsDataFrame, which is what we want.
class(wcape_wards_sp)[1] "SpatialPolygonsDataFrame"
attr(,"package")
[1] "sp"Having made the conversion we are ready to calculate some geographically weighted statistics, doing so for the High_income variable – the percentage of the population with income R614401 or greater in 2011 – in the example below.
gwstats <- gwss(wcape_wards_sp , vars = "High_income", bw = 10,
kernel = "bisquare",
adaptive = TRUE, longlat = T)The results are contained in the spatial data frame ($SDF),
head(gwstats$SDF)class : SpatialPolygonsDataFrame
features : 6
extent : 18.30766, 18.64221, -34.12601, -33.82513 (xmin, xmax, ymin, ymax)
crs : +proj=longlat +datum=WGS84 +no_defs
variables : 5
names : High_income_LM, High_income_LSD, High_income_LVar, High_income_LSKe, High_income_LCV
min values : 0.101829034109578, 0.0561016907606905, 0.00314739970620815, -0.283824535877161, 0.44823543363985
max values : 5.88774318923676, 2.92991675455044, 8.58441218859538, 1.7142999351663, 1.45252681718161 As well as the local means, the local standard deviations, variances, skews and coefficients of variation are included (the coefficient of variation is the ratio of the standard deviation to the mean). The local medians, interquartile ranges and quantile imbalances could also be added by including the argument quantile = TRUE in gwss() – see ?gwss.
The results are dependent on the data (of course) but also
The kernel matters…
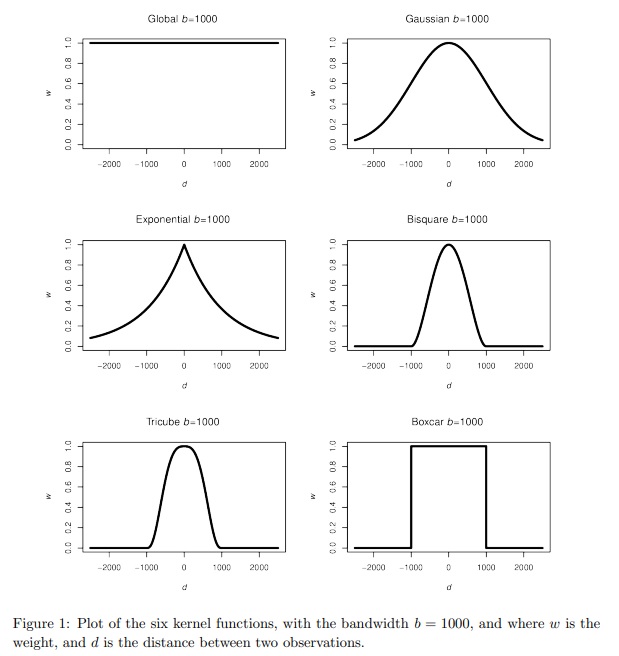Source: GWmodel: An R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models
… but it (usually) matters much less than the bandwidth, which controls the amount of spatial smoothing: the larger it is, the more neighbours are being averaged over. The trade-off is between bias and precision. A smaller bandwidth is less likely to average-out geographical detail in the data and should create geographically weighted statistics that are representative of the location at the centre of the kernel but are also dependent on a small number of observations, some or more of which could be in error or be unusual for that part of the map.
The following maps compare a bandwidth of \(bw = 10\) nearest neighbours to \(bw = 100\). If you zoom into the areas around the north of Cape Town you will see some of the differences. Note that the argument adaptive = TRUE sets the bandwidth to be in terms of nearest neighbours, else it would indicate a fixed distance of 10 metres. The advantage of using nearest neighbours is it allows for varying population densities. Otherwise, when using a fixed distance, more rural areas will tend to have fewer neighbours than urban ones because those rural areas are larger and more spaced apart.
gwstats <- gwss(wcape_wards_sp , vars = "High_income", bw = 10,
kernel = "bisquare",
adaptive = TRUE, longlat = T)
wcape_wards$bw10 <- gwstats$SDF$High_income_LM
gwstats <- gwss(wcape_wards_sp , vars = "High_income", bw = 100,
kernel = "bisquare",
adaptive = TRUE, longlat = T)
wcape_wards$bw100 <- gwstats$SDF$High_income_LM
wards2 <- pivot_longer(wcape_wards, cols = starts_with("bw"), names_to = "bw",
values_to = "GWmean")
tmap_mode("view")
tm_basemap("OpenStreetMap") +
tm_shape(wards2, names = "wards") +
tm_fill("GWmean", palette = "Reds", title = "%",
alpha = 0.7,
id = "District_1",
popup.vars = c("GW mean:" = "GWmean",
"Ward ID:" = "WardID"),
popup.format = list(digits = 1)) +
tm_borders() +
tm_facets(by = "bw") +
tm_legend(title =
"Geographically weighted % population with income R614401 or greater")
A nice feature of the facetting (tm_facets) in tmap is it has created two dynamically linked maps.
Here is a version of the maps using ggplot().
ggplot(wards2, aes(fill = GWmean), col = "transparent") +
geom_sf() +
scale_fill_distiller(type = "div", palette = "RdYlBu") +
facet_grid(~ bw) +
theme_minimal() +
labs(title = "Geographically weighted % population with income R614401 or greater")
### A slight tangent
You may note the use of the pivot_longer function from the tidyverse packages in the code above. To see what this does, take a look at,
wcape_wards |>
st_drop_geometry() |>
select(WardID, bw10, bw100) |>
arrange(WardID) |>
head(n = 3) WardID bw10 bw100
1 10101001 0.3868500 0.4349990
2 10101002 0.4108465 0.4435761
3 10101003 0.3742776 0.4254601Now compare it with,
wcape_wards |>
st_drop_geometry() |>
select(WardID, bw10, bw100) |>
pivot_longer(cols = starts_with("bw"), names_to = "bw",
values_to = "GWmean") |>
arrange(WardID) |>
head(n = 6)# A tibble: 6 × 3
WardID bw GWmean
<chr> <chr> <dbl>
1 10101001 bw10 0.387
2 10101001 bw100 0.435
3 10101002 bw10 0.411
4 10101002 bw100 0.444
5 10101003 bw10 0.374
6 10101003 bw100 0.425What you can see is that the two columns, bw10 and bw100 from the first table have been stacked into rows in the second. This takes the table from a wide format to a long one, hence the function name pivot_longer(). Doing this allows us to create the two linked plots by faceting on the bandwidth variable, bw, using tm_facets(by = "bw"). The reverse operation to pivot_longer() is pivot_wider() – see ?pivot_wider.
In the calculations above, the distances between the ward centroids that are used in the geographical weighting were calculated twice. First in gwss(wcape_wards_sp, vars = "High_income", bw = 10, ...) and then again in gwss(wcape_wards_sp, vars = "High_income", bw = 100, ...). Since those distances don’t actually change – the centroids are fixed so therefore are the distances between them – so we might have saved a little computational time by calculating the distance matrix in advance and then using it in the geographically weighted statistics. Curiously, though, it actually takes longer. I assume this is because the data set isn’t large enough to justify the extra step of saving the distances in a matrix and then passing that matrix to the gwss() function.
# Time to do the calculations without pre-calculating the distance matrix
system.time({
gwstats <- gwss(wcape_wards_sp , vars = "High_income", bw = 10,
kernel = "bisquare",
adaptive = TRUE, longlat = T)
wcape_wards$bw10 <- gwstats$SDF$High_income_LM
gwstats <- gwss(wcape_wards_sp , vars = "High_income", bw = 100,
kernel = "bisquare",
adaptive = TRUE, longlat = T)
wcape_wards$bw100 <- gwstats$SDF$High_income_LM
}) user system elapsed
0.039 0.001 0.041 # Time to do the calculations with the pre-calculated distance matrix
system.time({
coords <- st_coordinates(st_centroid(wcape_wards))
dmatrix <- gw.dist(coords, longlat = T)
gwstats <- gwss(wcape_wards_sp , vars = "High_income", bw = 10,
kernel = "bisquare",
adaptive = TRUE, longlat = T, dMat = dmatrix)
wcape_wards$bw10 <- gwstats$SDF$High_income_LM
gwstats <- gwss(wcape_wards_sp , vars = "High_income", bw = 100,
kernel = "bisquare",
adaptive = TRUE, longlat = T, dMat = dmatrix)
wcape_wards$bw100 <- gwstats$SDF$High_income_LM
}) user system elapsed
0.733 0.004 0.738 As observed in the maps above, the geographically weighted statistics are a function of the geographical weighting that largely is controlled by the bandwidth. This raises the question of which is the correct bandwidth to use? Unfortunately, the most honest answer is that there is no correct answer, although an automatic bandwidth selection might be tried by calibrating the statistics around the local means.
The following uses a cross-validation approach,
bw <- bw.gwr(High_income ~ 1, data = wcape_wards_sp,
adaptive = TRUE, kernel = "bisquare", longlat = T)Adaptive bandwidth: 256 CV score: 925.0618
Adaptive bandwidth: 166 CV score: 907.8583
Adaptive bandwidth: 110 CV score: 839.9751
Adaptive bandwidth: 75 CV score: 754.9144
Adaptive bandwidth: 54 CV score: 701.1287
Adaptive bandwidth: 40 CV score: 657.4657
Adaptive bandwidth: 32 CV score: 637.2662
Adaptive bandwidth: 26 CV score: 607.9657
Adaptive bandwidth: 23 CV score: 594.7227
Adaptive bandwidth: 20 CV score: 575.617
Adaptive bandwidth: 19 CV score: 575.2766
Adaptive bandwidth: 18 CV score: 566.5161
Adaptive bandwidth: 17 CV score: 561.563
Adaptive bandwidth: 17 CV score: 561.563 # The selected number of nearest neighbours:
bw[1] 17whereas the following uses an AIC corrected approach.
bw <- bw.gwr(High_income ~ 1, data = wcape_wards_sp,
adaptive = TRUE, kernel = "bisquare", longlat = T, approach ="AIC")Adaptive bandwidth (number of nearest neighbours): 256 AICc value: 1480.449
Adaptive bandwidth (number of nearest neighbours): 166 AICc value: 1473.901
Adaptive bandwidth (number of nearest neighbours): 110 AICc value: 1442.05
Adaptive bandwidth (number of nearest neighbours): 75 AICc value: 1398.784
Adaptive bandwidth (number of nearest neighbours): 54 AICc value: 1370.417
Adaptive bandwidth (number of nearest neighbours): 40 AICc value: 1345.457
Adaptive bandwidth (number of nearest neighbours): 32 AICc value: 1335.979
Adaptive bandwidth (number of nearest neighbours): 26 AICc value: 1320.554
Adaptive bandwidth (number of nearest neighbours): 23 AICc value: 1314.985
Adaptive bandwidth (number of nearest neighbours): 20 AICc value: 1303.224
Adaptive bandwidth (number of nearest neighbours): 19 AICc value: 1305.399
Adaptive bandwidth (number of nearest neighbours): 21 AICc value: 1306.969
Adaptive bandwidth (number of nearest neighbours): 19 AICc value: 1305.399
Adaptive bandwidth (number of nearest neighbours): 20 AICc value: 1303.224 bw[1] 20Both use a golden-section search method and, if you look at the output, both iterate to a very similar solution in a very similar set of steps. Bandwidths of 17 and 20 have been suggested. In practice, there is probably little between them so we may as well use the larger.
That automatic bandwidth selection applies only for the Western Cape wards, however. Recall earlier that the data were filtered (wards |> filter(ProvinceNa == "Western Cape") -> wcape_wards) with the partial explanation for doing so being to reduce run times. Another explanation is that there is no reason to assume that the spatial autocorrelation that is quantified by the bandwidth selection will be the same everywhere across the map. In fact, it varies from province to province:
bandwidths <- sapply(unique(wards$ProvinceNa), \(x) {
wards |>
filter(ProvinceNa == x) |>
as_Spatial() %>%
bw.gwr(High_income ~ 1, data = .,
adaptive = TRUE, kernel = "bisquare", longlat = T,
approach = "AIC") %>%
paste0("Bandwidth = ", .)
})bandwidths Free State Limpopo Mpumalanga Western Cape
"Bandwidth = 126" "Bandwidth = 25" "Bandwidth = 95" "Bandwidth = 20"
KwaZulu-Natal Eastern Cape North West Gauteng
"Bandwidth = 21" "Bandwidth = 24" "Bandwidth = 19" "Bandwidth = 19"
Northern Cape
"Bandwidth = 201" This suggests that fitting geographically weighted statistics to too large a study region is not desirable because there is little reason to presume that the same bandwidth should apply throughout it. The study region may be characterised by different spatial regimes.
So far we have been using the ward centroids as the points for which the geographically weighted statistics are calculated. There is no requirement to do this as they could be interpolated at any point within this study region. To demonstrate this, let’s reselect the wards in the Western Cape and convert them into a raster grid using the stars package. Stars is an abbreviation of spatial-temporal arrays and can be used for handling raster (gridded) data, as in the following example, which is taken from this introduction to the package.
if(!("stars" %in% installed)) install.packages("stars", dependencies = TRUE)
require(stars)
sat_image <- system.file("tif/L7_ETMs.tif", package = "stars")
sat_image <- read_stars(sat_image)
plot(sat_image, axes = TRUE)
We will use the st_rasterize function in stars to convert the geography of South Africa’s Western Cape into a regular grid.
wcape_wards |>
st_rasterize(nx = 100, ny = 100) |>
st_as_sf() ->
gridded
par(mai=c(0,0,0,0))
gridded |>
st_geometry() |>
plot()
We can now calculate the geographically weighted mean for each raster cell, with a bandwidth of 20 nearest neighbours.
gridded_sp <- as_Spatial(gridded)
gwstats <- gwss(wcape_wards_sp, gridded_sp, vars = "High_income",
bw = 20, kernel = "bisquare",
adaptive = TRUE, longlat = T)
gridded$GWmean <- gwstats$SDF$High_income_LM
ggplot(gridded, aes(fill = GWmean)) +
geom_sf(col = "light grey", size = 0) +
# size is the width of the raster cell border
scale_fill_continuous_c4a_seq(palette = "scico.lajolla") +
theme_minimal()
This ability to interpolate at any point within the study region provides a means to deal with missing values in the data. Contained in the wcape_wards data is a variable giving the average age of the population in each ward in 2011 but it contains 15 missing values:
summary(wcape_wards$age) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
24.90 27.95 29.80 30.91 33.00 51.30 15 The same observations also record NAs for the No_schooling variable. These are the rows of the data with missing values:
which(is.na(wcape_wards$age)) [1] 111 112 113 114 115 147 201 202 270 288 294 306 346 347 378which(is.na(wcape_wards$No_schooling)) [1] 111 112 113 114 115 147 201 202 270 288 294 306 346 347 378Missing value are a problem when fitting a regression model (line of best fit), for example. Usually they are simply omitted, as in the following case, where the output reports “(15 observations deleted due to missingness)”.
ols1 <- lm(No_schooling ~ age, data = wcape_wards)
summary(ols1)
Call:
lm(formula = No_schooling ~ age, data = wcape_wards)
Residuals:
Min 1Q Median 3Q Max
-9.7037 -2.1998 -0.5384 1.7687 13.2843
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 19.69367 1.14121 17.26 <2e-16 ***
age -0.38835 0.03657 -10.62 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.064 on 385 degrees of freedom
(15 observations deleted due to missingness)
Multiple R-squared: 0.2265, Adjusted R-squared: 0.2245
F-statistic: 112.8 on 1 and 385 DF, p-value: < 2.2e-16
An alternative approach to just automatically deleting them is to replace the missing values with a ‘safe’ alternative such as the mean of the values that are not missing for the variable. However, we could also replace each missing value with a locally interpolated mean which fits with the geographical context.
Here are the wards with missing age and no schooling values. These are the points that need to be interpolated.
wcape_wards |>
filter(is.na(age)) |>
as_Spatial() ->
missingThese are the wards with the values that serve as the data points.
wcape_wards |>
filter(!is.na(age)) |>
as_Spatial() ->
presentFortunately, the missing values seem to be fairly randomly distributed across the study region. It would be a problem if they were all geographically clustered together because interpolating their values from their neighbours would not be successful if their neighbours’ values were also missing!
par(mai=c(0, 0, 0, 0))
plot(present, border = "light grey")
plot(missing, col = "red", add = T)
We can, then, interpolate the missing values from the present ones and match them into the data using base R’s match() function, matching on their WardID. Note that I have done this twice, once for the age variable and once for No_schooling. This is to allow for the possibility of them having differently sized bandwidths from each other (which they do when using approach = "AIC", although not, as it happens, with the default approach = "CV").
bw <- bw.gwr(age ~ 1, data = present,
adaptive = TRUE, kernel = "bisquare", longlat = T,
approach = "AIC")
gwstats <- gwss(present, missing, vars = "age", bw = bw, kernel = "bisquare",
adaptive = TRUE, longlat = T)
mch <- match(missing$WardID, wcape_wards$WardID)
wcape_wards$age[mch] <- gwstats$SDF$age_LM
bw <- bw.gwr(No_schooling ~ 1, data = present,
adaptive = TRUE, kernel = "bisquare", longlat = T, approach = "AIC")
gwstats <- gwss(present, missing, vars = "No_schooling", bw = bw, kernel = "bisquare",
adaptive = TRUE, longlat = T)
wcape_wards$No_schooling[mch] <- gwstats$SDF$No_schooling_LMIt is useful to keep a note of which values are interpolated, so…
wcape_wards$interpolated <- FALSE
wcape_wards$interpolated[mch] <- TRUEThere should be 15 of them.
table(wcape_wards$interpolated)
FALSE TRUE
387 15 Now returning to our regression model, there are, of course, no longer any missing values and, reassuringly, no evidence that the interpolated values are significantly different from the rest in either their mean No_schooling value or in their effect of age upon No_schooling (I reach this conclusion by seeing that the variable interpolatedTRUE and the effect of the interpolation on age, age:interpolation are not significant).
ols2 <- update(ols1, . ~ . + interpolated*age)
summary(ols2)
Call:
lm(formula = No_schooling ~ age + interpolated + age:interpolated,
data = wcape_wards)
Residuals:
Min 1Q Median 3Q Max
-9.7037 -2.1709 -0.5446 1.7484 13.2843
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 19.69367 1.12855 17.450 <2e-16 ***
age -0.38835 0.03617 -10.738 <2e-16 ***
interpolatedTRUE -1.72125 10.95102 -0.157 0.875
age:interpolatedTRUE 0.02817 0.34961 0.081 0.936
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.03 on 398 degrees of freedom
Multiple R-squared: 0.2285, Adjusted R-squared: 0.2226
F-statistic: 39.28 on 3 and 398 DF, p-value: < 2.2e-16The geographically weighted mean acts as a smoothing (low pass) filter. We can see this if we apply it to a part of the satellite image from earlier. (If you try it on the whole image, you will be waiting a long time for the bandwidth to be calculated).
First we shall extract band 1 from the image, create a blank raster using the raster package and assign it the same values as from the image.
sat_image |>
slice(band, 1) |>
pull() -> vals
if(!("raster" %in% installed)) install.packages("raster", dependencies = TRUE)
dim(sat_image) x y band
349 352 6 st_bbox(sat_image) xmin ymin xmax ymax
288776.3 9110728.8 298722.8 9120760.8 r <- raster::raster(nrows = 352, ncol = 349,
xmn = 288776.3, xmx = 298722.8,
ymn = 9110728.8, ymx = 9120760.8)
raster::crs(r) <- "EPSG:31985"
# The image is 349 (row) by 352 (col) whereas the raster is
# 352 (col) by 349 (row) which is why the values are transposed, t(vals)
r <- raster::setValues(r, t(vals))Next we will crop out the top-left hand corner of the image, convert the coordinates and the attributes of those raster cells into a SpatialPointsDataFrame for use with the GWmodel functions and calculate the geographically weighted statistics:
r1 <- raster::crop(r, raster::extent(r, 1, 50, 1, 50))
pts <- as(r1, "SpatialPointsDataFrame")
bw <- bw.gwr(layer ~ 1, data = pts,
adaptive = TRUE, kernel = "bisquare", longlat = F,
approach = "AIC")Take a cup of tea and have a break, it will take a few minutes.
-----A kind suggestion from GWmodel development group
Adaptive bandwidth (number of nearest neighbours): 1552 AICc value: 17665.9
Adaptive bandwidth (number of nearest neighbours): 967 AICc value: 17492.74
Adaptive bandwidth (number of nearest neighbours): 604 AICc value: 17293.36
Adaptive bandwidth (number of nearest neighbours): 381 AICc value: 17083.12
Adaptive bandwidth (number of nearest neighbours): 242 AICc value: 16875.38
Adaptive bandwidth (number of nearest neighbours): 157 AICc value: 16641.81
Adaptive bandwidth (number of nearest neighbours): 103 AICc value: 16366.74
Adaptive bandwidth (number of nearest neighbours): 71 AICc value: 16052.66
Adaptive bandwidth (number of nearest neighbours): 50 AICc value: 15616.22
Adaptive bandwidth (number of nearest neighbours): 38 AICc value: 15240.6
Adaptive bandwidth (number of nearest neighbours): 29 AICc value: 14739.11
Adaptive bandwidth (number of nearest neighbours): 25 AICc value: 14546.43
Adaptive bandwidth (number of nearest neighbours): 21 AICc value: 14003.78
Adaptive bandwidth (number of nearest neighbours): 20 AICc value: 13950.83
Adaptive bandwidth (number of nearest neighbours): 18 AICc value: 13851.75
Adaptive bandwidth (number of nearest neighbours): 18 AICc value: 13851.75 gwstats <- gwss(pts, vars = "layer", bw = bw, kernel = "bisquare",
adaptive = TRUE, longlat = F)We can now compare the original image with the smoothed image.
r2 <- raster::setValues(r1, gwstats$SDF$layer_LM)
r <- st_as_stars(raster::addLayer(r1, r2))
ggplot() +
geom_stars(data = r) +
facet_wrap(~ band) +
coord_equal() +
theme_void() +
scale_fill_continuous_c4a_seq(name = "", palette = "scico.oslo")
However, it isn’t only the geographically weighted mean that is calculated. You could use the geographically weighted standard deviation, for example, as a high pass filter – a form of edge detection.
r2 <- raster::setValues(r1, gwstats$SDF$layer_LSD)
r <- st_as_stars(r2)
ggplot() +
geom_stars(data = r) +
coord_equal() +
theme_void() +
scale_fill_continuous_c4a_seq(name = "", palette = "scico.oslo")
You might spot that I have not loaded (required) the raster package in the code above but have accessed its functions via the :: notation; for example raster::setValues(). That is because if I do load the package, its select function will then mask a different function but with the same name in tidyverse’s dplyr. As I am only using the raster package very briefly, I didn’t think it was worth the potential confusion.
According to the regression model earlier, there is a negative correlation between the age of the population and the percentage without schooling. The correlation across the Western Cape is,
cor(wcape_wards$No_schooling, wcape_wards$age)[1] -0.4756981That is, however, the global correlation for what appears (below) to be a heteroscedastic relationship. Heteroscedastic means that the variation of the points is not constant around the regression line (line of best fit) – in the plot below, there is more variation to the left of the chart than to the right of it.
ggplot(data = wcape_wards, aes(x = age, y = No_schooling)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE)
Sometimes heteroscedasticity is indicative of a geographically varying relationship so let’s consider that by calculating and mapping the geographically weighted correlations between the two variables.
wcape_wards_sp <- as_Spatial(wcape_wards)
bw <- bw.gwr(No_schooling ~ age, data = wcape_wards_sp,
adaptive = TRUE, kernel = "bisquare", longlat = T)
gwstats <- gwss(wcape_wards_sp, vars = c("No_schooling", "age"), bw = bw,
kernel = "bisquare",
adaptive = TRUE, longlat = T)
wcape_wards$Corr_No_schooling.age <- gwstats$SDF$Corr_No_schooling.age
ggplot(wcape_wards, aes(fill = Corr_No_schooling.age)) +
geom_sf(col = "transparent") +
scale_fill_continuous_c4a_seq(name = "Correlation", palette = "hcl.blues3",
reverse = TRUE) +
theme_minimal() +
theme(legend.position="bottom") +
labs(
title = "Correlation between % No schooling and average age",
subtitle = "Geographically weighted (2011)"
)The local correlations range -0.868 to -0.105, with an interquartile range from -0.714 to -0.451:
summary(wcape_wards$Corr_No_schooling.age) Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.8679 -0.7136 -0.6294 -0.5801 -0.4506 -0.1054 If we add a little ‘cartographic know-how’ from an earlier session, we can identify that the correlation is stronger in and around Parow than it is in and around Blue Downs, for example.
if(!("remotes" %in% installed)) install.packages("remotes",
dependencies = TRUE)
if(!("ggsflabel" %in% installed)) remotes::install_github("yutannihilation/ggsflabel")
require(ggsflabel)
if(!file.exists("hotosm_zaf_populated_places_points.shp")) {
download.file("https://github.com/profrichharris/profrichharris.github.io/blob/main/MandM/boundary%20files/hotosm_zaf_populated_places_points_shp.zip?raw=true",
"cities.zip", mode = "wb", quiet = TRUE)
unzip("cities.zip")
}
read_sf("hotosm_zaf_populated_places_points.shp") |>
filter(place == "city" | place == "town") |>
st_join(wcape_wards) |>
# A spatial spatial join,
# giving the point places the attributes of the wards they fall in
mutate(population = as.integer(population)) |>
filter(!is.na(ProvinceNa) & population > 60000) ->
places
last_plot() +
geom_sf_label_repel(data = places, aes(label = name), alpha = 0.7,
force = 5, size = 2, max.overlaps = 20) +
xlab(element_blank()) +
ylab(element_blank())
In general, the correlation appears to be strongest in cities:
read_sf("hotosm_zaf_populated_places_points.shp") %>%
st_join(wcape_wards) %>%
st_drop_geometry %>%
group_by(place) %>%
summarise(meancorr = mean(Corr_No_schooling.age, na.rm = TRUE)) %>%
arrange(meancorr)# A tibble: 5 × 2
place meancorr
<chr> <dbl>
1 city -0.855
2 hamlet -0.620
3 isolated_dwelling -0.572
4 village -0.555
5 town -0.514We can use a randomisation procedure to determine whether any of the local summary statistics may be said to be significantly different from those obtained by chance. The randomisation procedure is found in the function, gwss.montecarlo() with a default number of nsim = 99 simulations. This isn’t very many but they are time-consuming to calculate and will be sufficient to demonstrate the process.
The following code chunk returns to the local mean percentages of high earners. It goes through the complete process of determining a bandwidth using the bw.gwr() function, then calculating the local and geographically weighted statistics using gwss(), determining the p-values under randomisation, using gwsss.montecarlo, then mapping the results. Very few of the results would be adjudged significant but a few are.
Calculating the p-values under randomisation takes some time so please be patient.
bw <- bw.gwr(High_income ~ 1, data = wcape_wards_sp,
adaptive = TRUE, kernel = "bisquare", longlat = T)Adaptive bandwidth: 256 CV score: 925.0618
Adaptive bandwidth: 166 CV score: 907.8583
Adaptive bandwidth: 110 CV score: 839.9751
Adaptive bandwidth: 75 CV score: 754.9144
Adaptive bandwidth: 54 CV score: 701.1287
Adaptive bandwidth: 40 CV score: 657.4657
Adaptive bandwidth: 32 CV score: 637.2662
Adaptive bandwidth: 26 CV score: 607.9657
Adaptive bandwidth: 23 CV score: 594.7227
Adaptive bandwidth: 20 CV score: 575.617
Adaptive bandwidth: 19 CV score: 575.2766
Adaptive bandwidth: 18 CV score: 566.5161
Adaptive bandwidth: 17 CV score: 561.563
Adaptive bandwidth: 17 CV score: 561.563 gwstats <- gwss(wcape_wards_sp , vars = "High_income", bw = bw,
kernel = "bisquare",
adaptive = TRUE, longlat = T)
p.values <- gwss.montecarlo(wcape_wards_sp, vars = "High_income", bw = bw,
kernel = "bisquare",
adaptive = TRUE, longlat = T)
p.values <- as.data.frame(p.values)
wcape_wards$High_income_LM <- gwstats$SDF$High_income_LM
wcape_wards$High_income_LM[p.values$High_income_LM > 0.025 &
p.values$High_income_LM < 0.975] <- NA
ggplot(wcape_wards, aes(fill = High_income_LM)) +
geom_sf(col = "transparent") +
scale_fill_distiller("%", palette = "Blues", na.value = "light grey",
direction = 1) +
theme_minimal() +
theme(legend.position="bottom") +
labs(
title = "Local mean percentage of higher earrners",
subtitle = "Geographically weighted (2011)"
)
A second example considers the local correlations between the No_schooling and age variables. Again, most of the correlations are insignificant but with a few exceptions.
bw <- bw.gwr(No_schooling ~ age, data = wcape_wards_sp,
adaptive = TRUE, kernel = "bisquare", longlat = T)gwstats <- gwss(wcape_wards_sp , vars = c("No_schooling", "age"), bw = bw,
kernel = "bisquare",
adaptive = TRUE, longlat = T)
p.values <- gwss.montecarlo(wcape_wards_sp, vars = c("No_schooling", "age"),
bw = bw, kernel = "bisquare",
adaptive = TRUE, longlat = T)
p.values <- as.data.frame(p.values)
wcape_wards$Corr_No_schooling.age <- gwstats$SDF$Corr_No_schooling.age
wcape_wards$Corr_No_schooling.age[p.values$Corr_No_schooling.age > 0.025 &
p.values$Corr_No_schooling.age < 0.975] <- NA
ggplot(wcape_wards, aes(fill = Corr_No_schooling.age)) +
geom_sf(col = "transparent") +
scale_fill_distiller("Correlation", palette = "Blues",
na.value = "light grey") +
theme_minimal() +
theme(legend.position="bottom") +
labs(
title = "Correlation between % No schooling and average age",
subtitle = "Geographically weighted (2011)"
)
We have the problem of repeating testing that we also had when looking for spatial hotspots in the session about spatial autocorrelation. The function p.adjust() could be used but we may wonder, as previously, where the methods are too conservative.
The following sections are not directly related to Geographically Weighted Statistics and can be skipped, if you wish.
The final part of this session is not about geographically weighted statistics or their applications but returns to thinking about mapping, to address the problem that some parts of some map are so small that their contents are almost illegible (too small to be seen).
The traditional and probably the most effective way to address the problem mentioned above is to add one or more inserts to the map to magnify the small areas. One way to do this is by using the cowplot package with ggplot2. The following example is based on this tutorial and maps the percentages of the populations who are relatively high earners in each ward.
First, we need to install and require the cowplot package.
if(!("cowplot" %in% installed)) install.packages("cowplot", dependencies = TRUE)
require(cowplot)Second, the part of the wards map to be included in the map insert is extracted, using st_crop.
wards_extract <- st_crop(wcape_wards, xmin = 18.2, xmax = 19, ymin = -34.3,
ymax = -33.5)
plot(st_geometry(wards_extract))
The bounding box for the extracted area is also obtained as it will be used as a feature in the final map (it will be drawn as a rectangle showing the geographical extent of the insert in the original map).
bbox <- st_as_sfc(st_bbox(wards_extract))Next, the main part of the map is created…
main_map <- ggplot(wcape_wards, aes(fill = High_income)) +
geom_sf(col = "transparent") +
scale_fill_binned_c4a_seq(name = "%", palette = "hcl.blues3") +
geom_sf(data = bbox, fill = NA, col = "black", size = 1.2) +
theme_minimal() +
theme(legend.position="bottom") +
labs(
title = "Percentage of the population who are higher earners",
subtitle = "(2011)"
)
plot(main_map)
…as is the map insert:
insert <- ggplot(wards_extract, aes(fill = High_income)) +
geom_sf(col = "transparent") +
scale_fill_binned_c4a_seq(palette = "hcl.blues3") +
geom_sf(data = bbox, fill = NA, col = "black", size = 1.2) +
theme_void() +
theme(legend.position = "none")
plot(insert)
Finally, the maps are brought together using cowplot’s ggdraw() and draw_plot() functions. We know that some of the values it shows are not necessarily significant under randomisation but we will include them here anyway, just of the purpose of demonstration.
ggdraw() +
draw_plot(main_map) +
draw_plot(insert, x = 0, y = 0.25, scale = 0.22) +
draw_label("Cape Town\nand\nsurrounding areas", x = 0.62, y = 0.78, size = 8)
The positioning of the map insert (x = ... & y = ...), the scaling of it, and the size and position of the label were all found by trial and error, using various values until I was happy with the results.
Another approach is to use what has been described as a visually balanced cartogram. A cartogram – of which there are lots of interesting examples on this website – usually works by distorting a map in a way that rescales the areas in proportion not to their physical size but by some other measured attribute such as their population count. Much of the motivation for this lies in political studies and mapping the results of an election wherein a traditional map can give a very distorted view of the outcome because of how much population density varies across a country. In the example below, rescaling the areas by population correctly shows that the 2020 US Presidential was not a Republican landslide, despite Trump’s baseless accusations!
Source: www.viewsoftheworld.net
The problem with cartograms is the distortion. Essentially, they are trading one visual problem (invisibility of small areas) for another (the amount of geographical distortion). The idea of a balanced cartogram comes from an awareness that sometimes it is sufficient just to make the small areas bigger and/or the big areas smaller, without causing too much geographical distortion. One way to achieve this is to scale the places by the square root of the original areas, as in the following example.
if(!("cartogram" %in% installed)) install.packages("cartogram",
dependencies = TRUE)
require(cartogram)
# Convert from longitude/latitude to a grid projection
wcape_wards %>%
st_transform(22234) %>%
mutate(area = as.numeric(st_area(.)),
w = as.numeric(sqrt(area))) ->
wards_prj
# Create the cartogram -- here a contiguous cartogram is used, see ?cartogram
# This might take a minute or two
wards_carto <- cartogram_cont(wards_prj, weight = "w", maxSizeError = 1.4,
prepare = "none")
ggplot(wards_carto, aes(fill = High_income)) +
geom_sf(col = "white", size = 0.1) +
scale_fill_binned_c4a_seq(name = "%", palette = "hcl.blues3") +
theme_minimal() +
theme(legend.position="bottom") +
labs(
title =
"Cartogram of the percentage of the population who are higher earners",
subtitle = "(2011)"
)
The results are ok, drawing attention to the wards with higher percentages of higher earners but clearly there is geographical distortion in the map, too.
The final approach to be considered here is what has been described as hexograms – a combination of tile maps and cartograms that make small areas bigger on the map but try and limit the geographic distortion. The original method also preserved typology (i.e. contiguous neighbours remained so in the final map) but is dated and very slow to operationalise as it was really just a proof of concept. A faster method but one that cannot guarantee to preserve typology is presented below. Don’t worry about the details especially. The code is included just to show you a method.
First, we need some functions to create the hexogram.
if(!("cartogram" %in% installed.packages()[,1])) install.packages("cartogram")
if(!("sf" %in% installed.packages()[,1])) install.packages("sf")
if(!("lpSolve" %in% installed.packages()[,1])) install.packages("lpSolve")
require(sf)
create_carto <- \(x, w = NULL, k = 2, itermax = 25, maxSizeError = 1.4) {
if(class(x)[1] != "sf") stop("Object x is not of class sf")
if(is.null(w)) x$w <- as.numeric(st_area(x))^(1/k)
cartogram::cartogram_cont(x, "w", itermax = itermax,
maxSizeError = maxSizeError, prepare = "none")
}
create_grid <- \(x, m = 6) {
bbox <- st_bbox(x)
ydiff <- bbox[4] - bbox[2]
xdiff <- bbox[3] - bbox[1]
n <- m * nrow(x)
ny <- sqrt(n / (xdiff/ydiff))
nx <- n / ny
nx <- ceiling(nx)
ny <- ceiling(ny)
grd <- st_sf(st_make_grid(x, n = c(nx, ny), square = FALSE))
}
grid_data <- \(x, grd, k = 2) {
x_pts <- st_centroid(st_geometry(x), of_largest_polygon = TRUE)
grd_pts <- st_centroid(grd)
cost.mat <- st_distance(x_pts, grd_pts)^k
row.rhs <- rep(1, length(x_pts))
col.rhs <- rep(1, nrow(grd_pts))
row.signs <- rep("=", length(x_pts))
col.signs <- rep("<=", nrow(grd_pts))
optimisation <- lpSolve::lp.transport(cost.mat, "min", row.signs, row.rhs,
col.signs, col.rhs)$solution
mch <- sapply(1:nrow(optimisation), \(i) which(optimisation[i, ] == 1))
grd <- st_sf(grd[mch,])
cbind(grd, st_drop_geometry(x))
}
create_layers <- \(x, grd) {
area <- sapply(1: nrow(x), \(i) {
y <- st_intersects(x[i, ], grd)[[1]]
if(i %in% y) {
if(length(y) == 1) return(st_area(x[i, ]))
if(length(y) > 1) {
area <- st_area(x[i, ])
overlaps <- y[-(y == i)]
area <- area - sum(st_area(st_intersection(st_geometry(x[i, ]),
st_geometry(grd[overlaps, ]))))
return(area)
}
} else {
return(0)
}
})
i <- which(area > 2*as.numeric(st_area(grd))[1])
list(x[i, ], grd[-i, ])
}Next, we run through the stages of its creation, which are to start with a balanced cartogram (create_carto()), then overlay that with a grid of hexagons (create_grid()), next assign places in the original map to a hexagon (grid_data()), then plot the results as two layers (create_layers()) to give a mash-up of the cartogram and the hexagons.
wards_carto <- create_carto(wards_prj)
grd <- create_grid(wards_carto)
wards_grid <- grid_data(wards_carto, grd)
wards_layers <- create_layers(wards_carto, wards_grid)
ggplot() +
geom_sf(data = wards_layers[[1]], aes(fill = High_income),
col = "white", size = 0.4) +
geom_sf(data = wards_layers[[2]], aes(fill = High_income),
col = "dark grey") +
scale_fill_binned_c4a_seq(name = "%", palette = "hcl.blues3") +
theme_minimal() +
theme(legend.position = "bottom") +
labs(
title = "Hexogram % of the population who are higher earners",
subtitle = "South African Western Cape (2011)"
)
I find the result quite visually appealing and it isn’t just me: a separate study has provided empirical evidence for the value of balanced cartograms and hexograms as a visualisation tool mapping spatial distributions. I have been playing around with a more sophisticated implementation of the code recently to try and map the changing ethnic diversity of all the census neighbourhoods in England and Wales.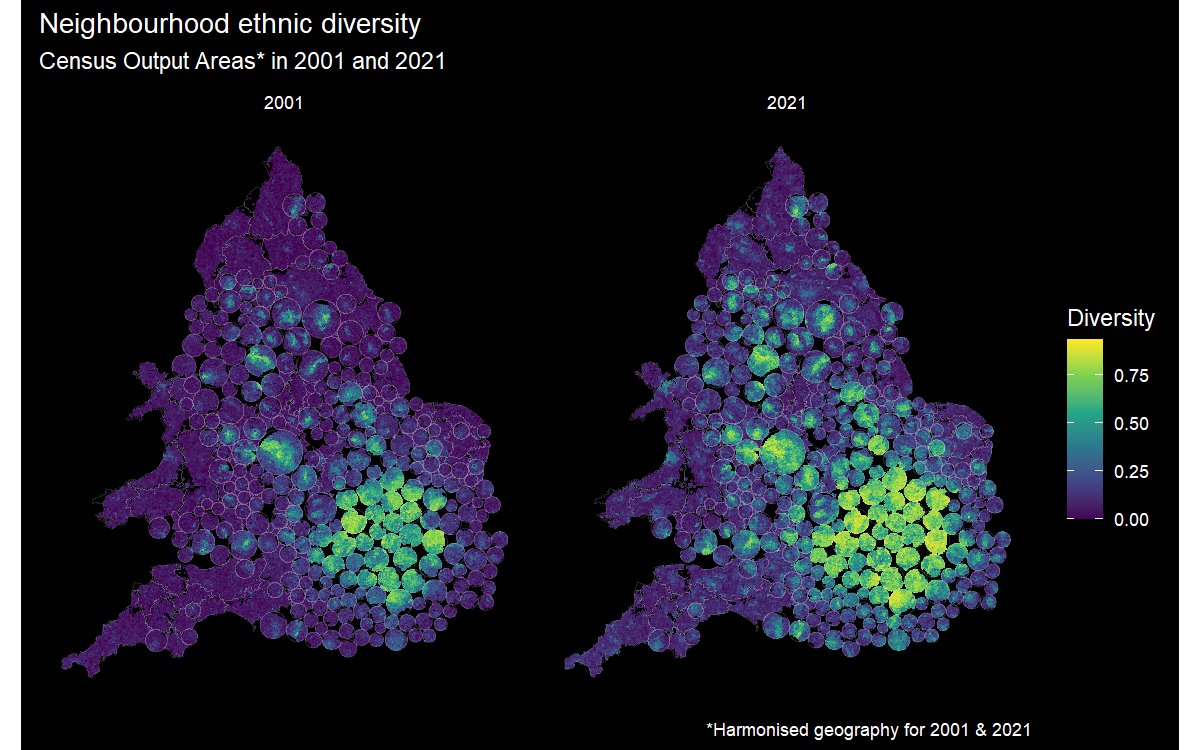
This session has introduced the concept of geographically weighted statistics to examine spatial heterogeneity in a measured variable and to allow for the possibility that its strength (and direction) of correlation with another variable varies from place-to-place. As such, these statistics are a form of local statistic, which is to say they can vary across the map. Sometimes, the parts of the map that we are interested in are small in relation to other parts, creating a problem of invisibility/legibility. Maps inserts, balanced cartograms and hexograms have been introduced as a means to address this visualisation problem.
Gollini I, Lu B, Charlton M, Brunsdon C & Harris P (2015). GWmodel: An R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models. Journal of Statistical Software, 63(17), 1–50. https://doi.org/10.18637/jss.v063.i17
Brunsdon C, Comber A, Harris P, Rigby J & Large A (2021). In memoriam: Martin Charlton. Geographical Analysis, 54(4), 713–4. https://doi.org/10.1111/gean.12309